Optimizers
- Momentum and Nestorov’s method improve convergence by normalizing the mean (first moment) of the derivatives
- Considering the second moments
- RMS Prop / Adagrad / AdaDelta / ADAM1
- Simple gradient and momentum methods still demonstrate oscillatory behavior in some directions2
- Depends on magic step size parameters (learning rate)
- Need to dampen step size in directions with high motion
- Second order term (use variation to smooth it)
- Scale down updates with large mean squared derivatives
- scale up updates with small mean squared derivatives
RMS Prop
- Notion
- The squared derivative is
- The mean squared derivative is
- This is a variant on the basic mini-batch SGD algorithm
- Updates are by parameter
- If using the same step over a long period,
- So
- Only the sign remain, similar to RProp
Adam
- RMS prop only considers a second-moment normalized version of the current gradient
- ADAM utilizes a smoothed version of the momentum-augmented gradient
- Considers both first and second moments
- Typically , initalize , so , will be very slow to update in the beginning
- So we need term to scale up in the beginning
Tricks
- To make the network converge better, we can consider the following aspects
- The Divergence
- Dropout
- Batch normalization
- Gradient clipping
- Data augmentation
Divergence
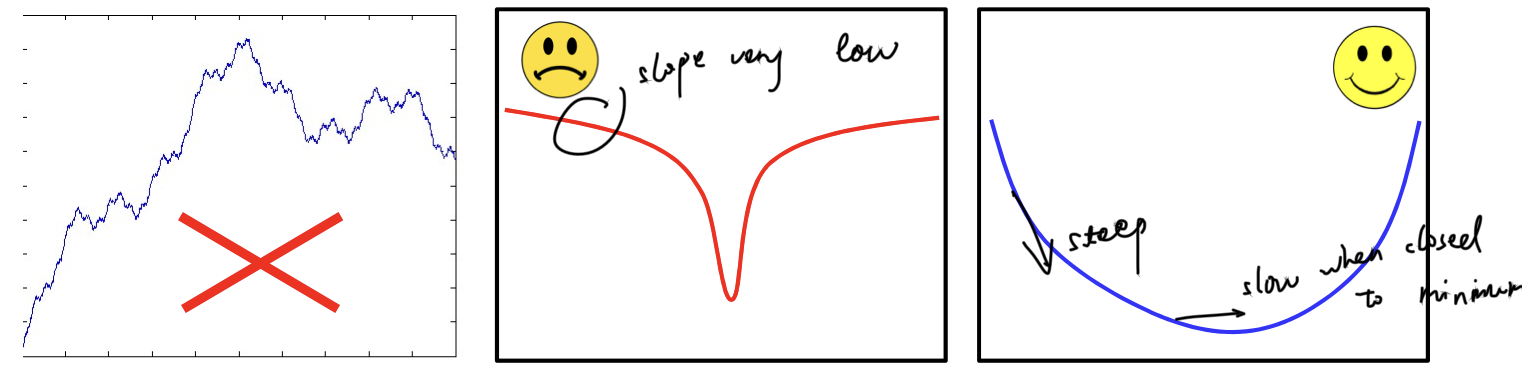
- What shape do we want the divergence function would be?
- Must be smooth and not have many poor local optima
- The best type of divergence is steep far from the optimum, but shallow at the optimum
- But not too shallow(hard to converge to minimum)
- The choice of divergence affects both the learned network and results
Common choices
- L2 divergence
KL divergence
L2 is particularly appropriate when attempting to perform regression
- Numeric prediction
- For L2 divergence the derivative w.r.t. the pre-activation of the output layer is :
- We literally “propagate” the error backward
- Which is why the method is sometimes called “error backpropagation”
The KL divergence is better when the intent is classification
- The output is a probability vector
Batch normalization
Covariate shifts problem
- Training assumes the training data are all similarly distributed (So as mini-batch)
- In practice, each minibatch may have a different distribution
- Which may occur in each layer of the network
- Minimize one batch cannot give the correction of other batches
Solution
- Move all batches to have a mean of 0 and unit standard deviation
- Eliminates covariate shift between batches
Batch normalization is a covariate adjustment unit that happens after the weighted addition of inputs (affine combination) but before the application of activation 5
Steps
- Covariate shift to standard position
Shift to right position
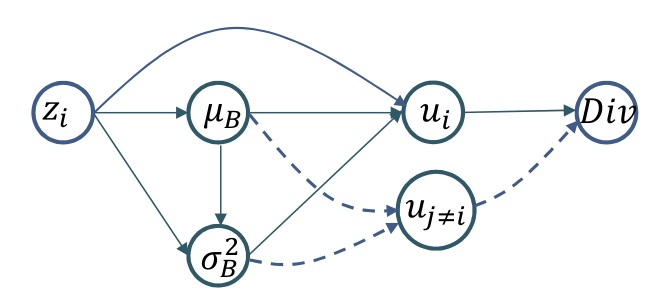
Backpropagation
- The outputs are now functions of and which are functions of the entire minibatch
- The divergence for each depends on all the within the mini-batch
- Is a vector function over the mini-batch
- Using influence diagram to caculate derivatives3
Goal
- We need to caculate the learnable parameters , and the affine combination
- So we need extra
Preparation
For the first term
First caculate
, so the first term =
For the second term
- Caculate
- And
- So the second term =
Finally for the third term
- Caculate
- The last term is zero, and because
- So the third term =
- Overall
Inference
- On test data, BN requires and
- We will use the average over all training minibatches
- Note: these are neuron-specific
- are obtained from the final converged network
- The 𝐵/(𝐵 − 1) term gives us an unbiased estimator for the variance
What can it do
- Improves both convergence rate and neural network performance
- Anecdotal evidence that BN eliminates the need for dropout
- To get maximum benefit from BN, learning rates must be increased and learning rate decay can be faster
- Since the data generally remain in the high-gradient regions of the activations
- e.g. For sigmoid function, move data to the linear part, the gradient is high
- Also needs better randomization of training data order
Smoothness
- Smoothness through network structure
- MLPs are universal approximators
- For a given number of parameters, deeper networks impose more smoothness than shallow&wide ones
- Each layer restricts the shape of the function
- Smoothness through weight constrain
Regularizer
- The "desired” output is generally smooth
- Capture statistical or average trends
- Overfitting
- But an unconstrained model will model individual instances instead
- Why overfitting?4
- Using a sigmoid activation, as increases, the response becomes steeper
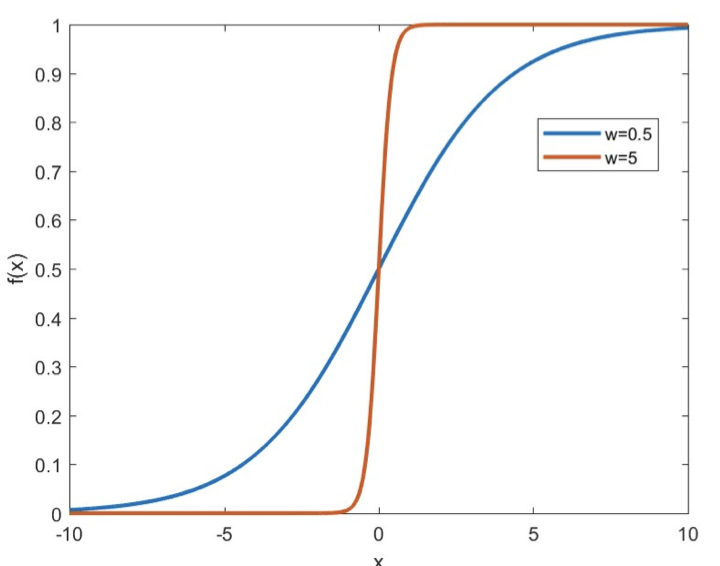
- Constraining the weights to be low will force slower perceptrons and smoother output response
- Regularized training: minimize the loss while also minimizing the weights
- is the regularization parameter whose value depends on how important it is for us to want to minimize the weights
- Increasing assigns greater importance to shrinking the weights
- Make greater error on training data, to obtain a more acceptable network
Dropout
- “Dropout” is a stochastic data/model erasure method that sometimes forces the network to learn more robust models
- Bagging method
- Using ensemble classifiers to improve prediction
Dropout
- For each input, at each iteration, “turn off” each neuron with a probability
- Also turn off inputs similarly
Backpropagation is effectively performed only over the remaining network
- The effective network is different for different inputs
- Effectively learns a network that averages over all possible networks (Bagging)
Dropout as a mechanism to increase pattern density
- Dropout forces the neurons to learn “rich” and redundant patterns
- E.g. without dropout, a noncompressive layer may just “clone” its input to its output
- Transferring the task of learning to the rest of the network upstream
Implementation
The expected output of the neuron is
During test, push the a to all outgoing weights
- So
- Instead of multiplying every output by all weights by , multiply all weight by
- Alternate implementation
- During training, replace the activation of all neurons in the network by
- Use as the activation during testing, and not modify the weights

More tricks
- Obtain training data
- Use appropriate representation for inputs and outputs
- Data Augmentation
- Choose network architecture
- More neurons need more data
- Deep is better, but harder to train
- Choose the appropriate divergence function
- Choose regularization
- Choose heuristics
- batch norm, dropout ...
- Choose optimization algorithm
- Adagrad / Adam / SGD
- Perform a grid search for hyper parameters (learning rate, regularization parameter, …) on held-out data
- Train
- Evaluate periodically on validation data, for early stopping if required
1. A good summary of recent optimizers can be seen in here. ↩
2. Animations for optimization algorithms ↩
3. A simple and clear demostration of 2 variables in a single network ↩
4. The perceptrons in the network are individually capable of sharp changes in output ↩
5. Batch normalization in Neural Networks ↩